这学期选了卜老师的Algorithm Design and Analysis课,简单的分析一下Divide And Conquer课后留的题目
1 Divide and Conquer
You are interested in analyzing some hard-to-obtain data from two separate databases. Each database contains n numerical values, so there are 2n values total and you may assume that no two values are the same. You’d like to determine the median of this set of 2n values, which we will define here to be the nth smallest value.
However, the only way you can access these values is through queries to the databases. In a single query, you can specify a value k to one of the two databases, and the chosen database will return the kth smallest value that it contains. Since queries are expensive, you would like to compute the median using as few queries as possible.
Give an algorithm that finds the median value using at most O(log n) queries.
-
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
-
What if all houses are arranged in a circle?
分析:
我们将两个数据库分别命名为A和B。由于A和B的长度均为n,所以总共的长度为2n,这里定义的中位数位是第n小的元素,而不是求第(2n + 1) / 2的元素和第(2n + 1) / 2 + 1的元素的均值。由于A和B能查询分别查询其第K个元素是什么(可以看成已经排好顺序的数组)。我们要找的是数据库A 和数据库B融合后的数据库C的中位数C(n)。我们先分别查询数据库A的中位数A(n/2)和数据库B的中位数B(n/2)。
- 如果A(n/2)<B(n/2),那么有:
(1)B(n/2)>A(1),A(2),…,A(n/2) B(n/2)>B(1),B(2),…B(n/2-1) B(n/2)将会比n-1个数要大,所以B(n/2)>=C(n),所以C(n)不会出现在B(n/2+1), B(n/2+2)…B(n)中。
(2)A(n/2)<B(n/2), B(n/2+1),…B(n) A(n/2)<A(n/2+1), A(n/2+2),…A(n) A(n/2)将会比n-1个元素要小,所以A(n/2)<=C(n),所以C(n)不会出现在A(1),A(2),,…A(n/2-1)之中。 - 相反的,如果A(n/2)>B(n/2),那么有:
(1)A(n/2)>B(1),B(2),…B(n/2) A(n/2)>A(1),A(2),…A(n/2-1) A(n/2)<=C(n),不用考虑A(n/2+1),A(n/2+2),…,a(n)的部分了。
(2)B(n/2)<A(n/2),A(n/2+1),…,A(n) B(n/2)<B(n/2+1),B(n/2+2),…,B(n)
所以B(n/2)<=C(n),所以C(n)不会出现在B(1), B(2)…B(n/2-1)中。
综上所述:我们先找出两个数据库的中位数,然后进行比较,根据比较的结果,将中位数所在的范围缩小一半。然后继续寻找剩下区间的中位数,再次缩小一半,经过 ${log_2{n}}$ 次数的缩小,最终得到两个数字,选择其中较小的即为数据库c的中位数。
pseudo-code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Find Median for two joint database()
k1=k2=n/2 #先比较A和B的中位数
for i=2 to log2 n:
AK=Querydatabase(A,k1)
BK=Querydatabase(B,k2)
If AK> BK
Then k1=k1-n/2i #下次查找查找数据库A上半部分的中位数
k2=k2+n/2i #下次查找查找数据库B下半部分的中位数
Else:
k1=k1+n/2i
k2=k2-n/2i
End if
End for
return min(AK,BK)
Subproblem reduction graph:
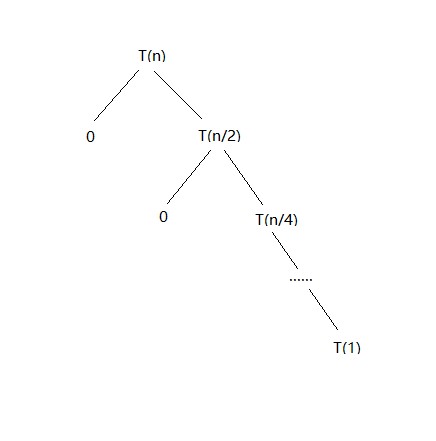
Prove the correctness:
- 在程序初始的时候,k1=k2=n/2,它们它们分别是子集A和子集B的中位数。
- 假设A的中位数AK小于B的中位数BK,两个数据库结合的数据库C的中位数应该存在于A的较大的一半或者B的较小的一半。接着继续比较这两个子区间的中位数,在这两个子区间内继续寻找,继续缩小查找范围。在每一次缩小查找中位数的区间的时候,总能排除掉中位数不可能存在的区间,将查找区间缩小为原来的1/2。
- 最后,i=log2 n,经过log2 n的查找,AK和BK分别是数据库C第n小和第n+1小的两个数,根据题目中关于中位数的定义,取其中较小的即可。
Analyse the complexity of your algorithm:
对数据库的查询总的时间复杂度是T(n),在每个循环中我们将问题的规模转化为原问题规模的1/2和两次对数据库的查询。因此有T(n)=T(n/2)+2,时间复杂度为$O(log_n)$。
2 Divide and Conquer
Consider an n-node complete binary tree T, where n = 2d -1 for some d. Each node v of T is labeled with a real number xv. You may assume that the real numbers labeling the nodes are all distinct. A node v of T is a local minimum if the label xv is less than the label xw for all nodes w that are joined to v by an edge.
You are given such a complete binary tree T, but the labeling is only specified in the following implicit way: for each node v, you can determine the value xv by probing the node v. Show how to find a local minimum of T using only O(log n) probes to the nodes of T.
分析:
完全二叉树的子树仍然是完全二叉树,任何一棵完全二叉树都有局部最小值。从完全二叉树的根节点出发,探查它的两个孩子节点,如果它的两个孩子节点均比它大,则返回根节点的值;否则就递归查找两个孩子中值最小的那一个,直到没有孩子节点。
pseudo-code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
find-local-minimum(T,rootnode v):
if v->left child ==None&&v->right child==None:
return v
else:
l=v->left child
r=v->right child
if(v<l&&v<r)
return v
else:
v=min(l,r)
find-local-minimum(T,v)
end if
end if
subproblem reduction graph:
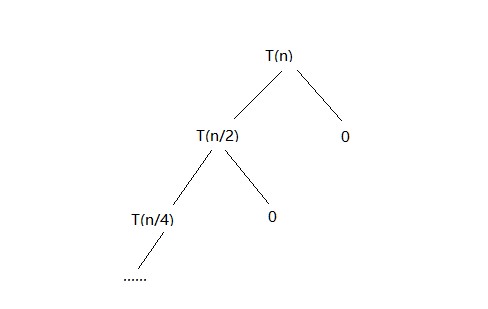
Prove the correctness:
- 在程序初始的时候,我们从根节点开始程序,将根节点的值与它的左右孩子进行比较,返回两个孩子当中最小的那一个。
- 假设两个孩子节点当中最小的是右孩子节点,继续将右孩子节点赋给v,继续比较节点v和它的两个孩子节点,一直递归下去,直到得到的节点的值比它的两个孩子节点都要小为止或者没有孩子节点为止。
- 最后,返回的v的值一定是局部最小的,而且一定是整个遍历路径当中最小的。
Analyse the complexity:
在最坏的情况下,从完全二叉树的根节点遍历至最后一层的叶子节点,因此有T(n)=T(n/2)+cn。完全二叉树的深度决定了程序时间所要执行的时间。具有n个节点的完全二叉树的深度为$log_2(n+1)$,因此,时间复杂度为$O(log_n)$。
3 Divide and Conquer
Recall the problem of finding the number of inversions. As in the course, we are given a sequence of n numbers a1,··· ,an, which we assume are all distinct, and we define an inversion to be a pair i < j such that $a_i$ > $a_j$.
We motivated the problem of counting inversions as a good measure of how different two orderings are. However, one might feel that this measure is too sensitive. Let’s call a pair a significant inversion if $i < j$ and $a_i$ > $3a_j$. Given an $O(nlog_n)$ algorithm to count the number of significant inversions between two orderings.
分析:
与利用归并排序求逆序数的个数类似,在递归调用的时候时候分别计算各一半的逆序数,在进行合并时再分别计算位于左边和右边的逆序数,在递归的过程中,对序列进行分割时,直到序列中剩一个数时就无法再分了。在合并的过程中,比较左边序列的L[i]与右边序列的R[j],如果L[i]>3* R[j],那么L[i]后面的数字都要比3* R[j]要大,就不需要再比较了,逆序数的个数增加了子数组L的长度减i个。
pseudo-code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Sort-and-count(A):
Divide A into two sub-sequences L and R;
(RCL,L)= Sort-and-count(L);
(RCR,L)= Sort-and-count(R);
(C,A)=Merge-and-count(L,R);
return (RC=RCL+RCR+C,A);
Merge-and-count(L,R)
Merge-and-count(L,R)
RC=0;i=0;j=0;
for k=0 to L+R-1:
if (L[i]> R[j])
A[k]=R[j];
if( L[i] > 3R[j])
RC+=(n/2-i)
end if
j++;
else
A[k]=L[i]
i++;
end if
end for
return (RC,A)
subproblem reduction graph:
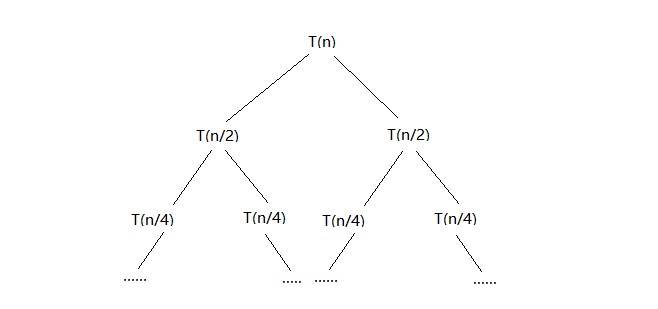
Prove the correctness:
该算法在归并排序的基础上,在L[i] > R[j]的情况下,添加了一个L[i] > 3R[j]的判断过程,用来求解significant inversion的个数,其和归并过程复杂度一样,都为O(n)。与归并排序的思路类似,不断的将一个序列将分割为为两个子序列,直到序列中剩一个数时就无法再分了;在合并的过程中,比较左边序列的L[i]与右边序列的R[j],如果L[i]>3* R[j],那么显然,L[i]>3* R[j+1,……],L[i]后面的数字都要比3* R[j]要大,该算法是正确的。
Analyse the complexity:
由于每次递归都将问题的规模折半,再加上将子问题结合的时间,因此有T(n)=2T(n/2)+cn。其中,Merge-and-count(L,R)函数的时间复杂度为cn。由Master Theorem,时间复杂度为$O(nlog_n)$。